Fri 21 Nov 2003
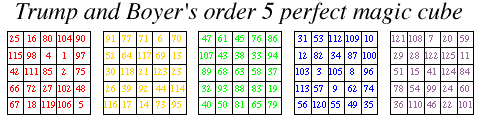
November 18, 2003–This week, German mathematician and teacher Walter Trump and French mathematician Christian Boyer announced the discovery of a perfect magic cube of order 5, thus settling the long-open question of the existence of such a cube.
If only the above set of 3n2+4 diagonals sum to the magic constant, a cube is said to be semiperfect. If, however, the rows, columns, pillars, space diagonals, and diagonals of each n x n orthogonal slice (for a total of 6n orthogonal diagonals) sum to the same number, the cube is called perfect.
There is a trivial perfect magic cube of order one, but no perfect cubes exist for orders 2-4 (Schroeppel 1972, Gardner 1988). It was long not known if perfect (normal) magic cubes of orders 5 or 6 could exist (Wells 1986, p. 72), although Schroeppel (1972) and Gardner (1988) noted that any normal perfect magic cube of order 5 must have a central value of 63.
Then, on November 13, 2003, Trump and Boyer discovered the order five perfect magic cube illustrated above (Schroeppel 2003, Boyer 2003). As expected, this cube has magic constant 315 and central value 63. The method used by Trump and Boyer consisted of constructing auxiliary cubes of order three. These cubes were central symmetrical, meaning that all 13 lines of three numbers including the central number satisfied the identity x + y + 63 = 189, as well as a number of other partial magic characteristics. Using these auxiliary cubes, Trump and Boyer performed a large computer search to fill in the missing numbers, mainly using complementary numbers x + y + 189 = 315. As a result of this procedure, there are many symmetries present in this cube. After several weeks of computer searches and the construction of more than 80,000 different auxiliary cubes of order 3, Trump and Boyer found the first known order 5 perfect magic cube (Boyer 2003).
Trump and Boyer’s discovery followed closely Trump’s September 1, 2003 discovery of the first known perfect magic cube of order six, illustrated above. This cube was found using techniques similar to those used to attack the order 5 cube (Boyer 2003). As csan be directly verified, this cube has magic constant 651.
Happily, magic cube enthusiasts need have no fear that magic cubes hold no more mysteries or challenges. Even though perfect magic cubes of orders five and six are now known, there is still much that remains unknown about magic cubes. For example, a magic cube is called bimagic if it and the cube obtained by squaring each of its entries are both magic (although in this case, the squares cube is naturally no longer normal). The smallest known bimagic cube is of order 16, and the smallest known perfect bimagic cube is of order 32. Similarly, the smallest known trimagic cube is of order 64, and the smallest known perfect trimagic cube is of order 256 (Boyer, Heinz). Since no smaller examples have yet been discovered, this area of investigation remains wide open to enterprising “cubists”!